C#实现马尔科夫模型例子
已知條件:三個(gè)缸N狀態(tài),每個(gè)缸中不同顏色球的個(gè)數(shù)M狀態(tài)值,時(shí)間軸T,觀察值序列O
參數(shù):狀態(tài)值序列,轉(zhuǎn)移概率序列
求:概率
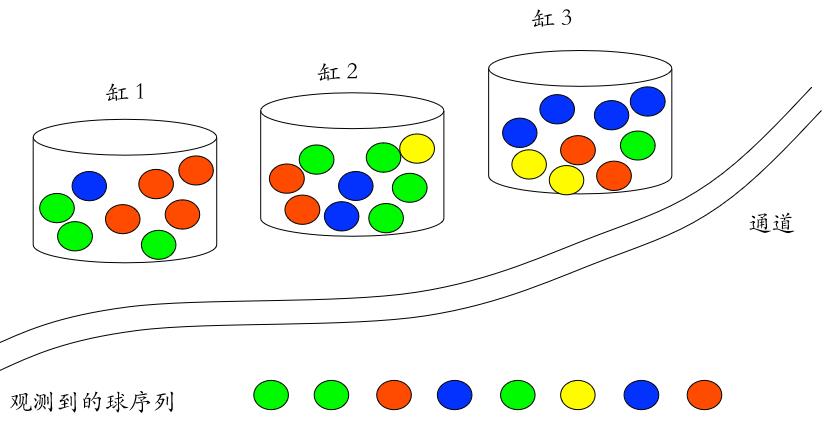
后臺(tái)代碼如下
已知條件:三個(gè)缸N狀態(tài),每個(gè)缸中不同顏色球的個(gè)數(shù)M狀態(tài)值,時(shí)間軸T,觀察值序列O
參數(shù):狀態(tài)值序列,轉(zhuǎn)移概率序列
求:概率
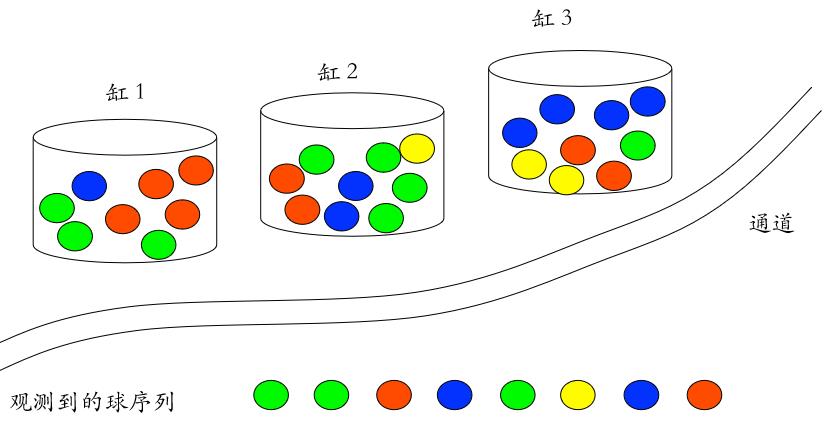
后臺(tái)代碼如下
const int N = 3, M = 4;//N狀態(tài),M狀態(tài)值 (0橙色,1綠色,2藍(lán)色,3黃色)
public int[] O = { 1, 1, 0, 2, 1, 3, 2, 0 };//觀察值序列
public double[,] A = new double[N, N];//初始一個(gè)三行三列的二維數(shù)組(狀態(tài)轉(zhuǎn)移概率)
public double[,] B = new double[N, M];//初始一個(gè)三行四列的二維數(shù)組(觀察值的概率矩陣)
public double[] PI = { 1.0 / 3.0, 1.0 / 3.0, 1.0 / 3.0 };//初始化概率 10
#region 獲取觀察值概率
/// <summary>
/// 獲取觀察值概率
/// </summary>
public void GetB()
{
//第一缸球的顏色
double[] one = { 4, 3, 1, 0 };
//第二缸球的顏色
double[] two = { 2, 4, 2, 1 };
//第一缸球的顏色
double[] three = { 2, 1, 4, 2 };
//每個(gè)缸中球的總數(shù)量
int[] count = { 8, 9, 9 };
for (int i = 0; i < 4; i++)
{
B[0, i] = one[i] / count[0];
B[1, i] = two[i] / count[1];
B[2, i] = three[i] / count[2];
}
}
#endregion
#region 獲取概率P值 zhy
/// <summary>
/// 獲取概率P值
/// </summary>
/// <param name="Q">狀態(tài)值序列(0第一個(gè)缸,1第二個(gè)缸,2第三個(gè)缸)</param>
/// <param name="A">轉(zhuǎn)移概率</param>
/// <returns></returns>
public double GetP(string Q, string A)
{
GetA(A);
GetB();
int[] q = GetQ(Q);
//時(shí)間軸
int T = 8;
//初始概率Q[0]:第一缸, O[0]:第一個(gè)球
double p = PI[q[0]] * B[q[0], O[0]];
for (int i = 1; i < T; i++)
{
//this.A:q[i-1]取上一個(gè)剛,q[i]取當(dāng)前缸,然后獲得轉(zhuǎn)移概率
//B:q[i]取當(dāng)前缸,O[i]取缸中哪個(gè)顏色的球
p *= this.A[q[i - 1], q[i]] * B[q[i], O[i]];
}
return p;
}
#endregion
#region 獲取狀態(tài)值序列 zhy
/// <summary>
/// 獲取狀態(tài)值序列
/// </summary>
/// <param name="Q">狀態(tài)值字符串</param>
/// <returns>狀態(tài)值數(shù)組</returns>
public int[] GetQ(string Q)
{
int[] q = null;
if (Q.TrimEnd(',').IndexOf(',') > 0)
{
//獲得狀態(tài)序列
string[] zhuangtai = Q.TrimEnd(',').Split(',');
q = new int[zhuangtai.Length];
for (int i = 0; i < zhuangtai.Length; i++)
{
q[i] = Convert.ToInt32(zhuangtai[i]);
}
}
else
{
q = new int[1];
q[0] = Convert.ToInt32(Q);
}
return q;
}
#endregion
#region 獲取轉(zhuǎn)移概率序列 zhy
/// <summary>
/// 獲取轉(zhuǎn)移概率序列
/// </summary>
/// <param name="A">轉(zhuǎn)移概率字符串</param>
public void GetA(string A)
{
if (A.TrimEnd(',').IndexOf(',') > 0)
{
string[] gailv = A.TrimEnd(',').Split(',');
//獲取A的轉(zhuǎn)移概率的二維數(shù)組
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
this.A[i, j] = Convert.ToDouble(gailv[3 * i + j]);
}
}
}
}
#endregion
html如下:
<span>請(qǐng)輸入狀態(tài)值序列 : </span><input type="text" id="zhuangtaizhi" value="0,2,1,1,2,0,0,1" /><span> 多個(gè)值請(qǐng)使用","隔開(kāi)(0第一缸,1第二缸,2第三缸)</span><br /><br />
<span> a11-a13 :</span>
<input type="text" id="a11_a13" value="0.25,0.45,0.2" /><span> 請(qǐng)輸入第一缸的轉(zhuǎn)移概率以","隔開(kāi),三值相加等于1</span><br /><br />
<span> a21-a23 :</span>
<input type="text" id="a21_a23" value="0.1,0.85,0.15" /><span> 請(qǐng)輸入第二缸的轉(zhuǎn)移概率以","隔開(kāi),三值相加等于1</span><br /><br />
<span> a31-a33 :</span>
<input type="text" id="a31_a33" value="0.14,0.55,0.31" /><span> 請(qǐng)輸入第三缸的轉(zhuǎn)移概率以","隔開(kāi),三值相加等于1</span><br /><br />
<input type="button" value="計(jì)算" onclick="count()" />
<div style="display:none;" id="jieguo">
<span>概率為:</span><span id="gailv"></span>
</div>
js如下
function count() {
var zhuangtaizhi = $.trim($("#zhuangtaizhi").val());
var a11_a13 = $.trim($("#a11_a13").val());
var a21_a23 = $.trim($("#a21_a23").val());
var a31_a33 = $.trim($("#a31_a33").val());
if (zhuangtaizhi == "") {
alert("請(qǐng)輸入狀態(tài)值序列");
return;
}
if (a11_a13 == "") {
alert("請(qǐng)輸入a11-a13的轉(zhuǎn)移概率");
return;
}
if (a21_a23 == "") {
alert("請(qǐng)輸入a21-a23的轉(zhuǎn)移概率");
return;
}
if (a21_a23 == "") {
alert("請(qǐng)輸入a21-a23的轉(zhuǎn)移概率");
return;
}
var zhuanyigailv = a11_a13 + "," + a21_a23 + "," + a31_a33;
$.post("/YinMa/GetP", { Q: zhuangtaizhi, A: zhuanyigailv }, function (msg) {
$("#gailv").html(msg);
$("#jieguo").show();
});
}