Python之scipy模块
一 簡單介紹
SciPy是基于NumPy開發的高級模塊，它提供了許多數學算法和函數的實現，用于解決科學計算中的一些標準問題。例如數值積分和微分方程求解，擴展的矩陣計算，最優化，概率分布和統計函數，甚至包括信號處理等。
作為標準科學計算程序庫，SciPy類似于Matlab的工具箱，它是Python科學計算程序的核心包，它用于有效地計算NumPy矩陣，與NumPy矩陣協同工作。
SciPy庫由一些特定功能的子模塊構成，如下表所示：
作為標準科學計算程序庫，SciPy類似于Matlab的工具箱，它是Python科學計算程序的核心包，它用于有效地計算NumPy矩陣，與NumPy矩陣協同工作。
SciPy庫由一些特定功能的子模塊構成，如下表所示：
| 模塊 | 功能 |
| cluster | 矢量量化 / K-均值 |
| constants | 物理和數學常數 |
| fftpack | 傅里葉變換 |
| integrate | 積分程序 |
| interpolate | 插值 |
| io | 數據輸入輸出 |
| linalg | 線性代數程序 |
| ndimage | n維圖像包 |
| odr | 正交距離回歸 |
| optimize | 優化 |
| signal | 信號處理 |
| sparse | 稀疏矩陣 |
| spatial | 空間數據結構和算法 |
| special | 任何特殊數學函數 |
| stats | 統計 |
import numpy as np from scipy
import stats
以上代碼表示從SciPy模塊中導入stats子模塊，SciPy的其他子模塊導入方式與之相同，限于機器學習研究領域及篇幅限制，本章將重點介紹linalg、optimize、interpolate及stats模塊。
2.1 線性代數linalg模塊
linalg是Linear Algebra的縮寫，NumPy和SciPy都提供了線性代數函數庫linalg，SciPy的線性代數庫比NumPy更加全面。
（1）基本運算
linalg包含了許多方陣（包括矩陣）的基本運算函數，scipy.linalg.det()函數計算方陣的行列式，示例代碼：
>>> from scipy import linalg
>>> arr = np.array([[1, 2], [3, 4]])
>>> linalg.det(arr) -2.0
>>> arr = np.array([[3, 2],[6, 4]])
>>> linalg.det(arr) 0.0
>>> linalg.det(np.ones((3, 4)))
#無論行列式還是逆矩陣只適用于n階矩陣的求解
Traceback (most recent call last):
...
ValueError: expected square matrix
scipy.linalg.inv()函數計算方陣的逆，示例代碼：
>>> arr = np.array([[1, 2], [3, 4]])
>>> iarr = linalg.inv(arr)
>>> iarr
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>>np.allclose(np.dot(arr, iarr), np.eye(2))
#numpy.allclose()函數用于比較兩方陣所有對應元素值，如果完全相同返回真(True)，否則返回假(False)
True
以下計算奇異陣（行列式為0）的逆，其結果將會報錯（LinAlgError），示例代碼：
>>>arr = np.array([[3, 2], [6, 4]])
>>>linalg.inv(arr)
Traceback (most recent call last):
...
...LinAlgError: singular matrix
scipy.linalg.norm()函數計算方陣的范數，示例代碼：
>>>A = np.matrix(np.random.random((2, 2)))
>>>A >>>linalg.norm(A) #默認2范數
>>>linalg.norm(A, 1) #1范數
>>>linalg.norm(A, np.inf) #無窮范數
（2）解線性方程組
scipy.linalg.solve(A,b)和numpy.linalg.solve(A,b)可以用來解線性方程組Ax=b，即計算x=A-1b。這里，A是mm的方形矩陣，x和b是長為m的向量。有時候A是固定的，需要對多組b進行求解，因此第二個參數也可以是mn的矩陣B。這樣計算出來的X也是m*n的矩陣，相當于計算A-1B。
在一些矩陣公式中經常會出現類似于A-1B的運算，它們都可以用solve(A, B)計算，這要比直接逆矩陣然后做矩陣乘法更快捷一些，下面的程序比較solve()和逆矩陣的運算速度，示例代碼：
在一些矩陣公式中經常會出現類似于A-1B的運算，它們都可以用solve(A, B)計算，這要比直接逆矩陣然后做矩陣乘法更快捷一些，下面的程序比較solve()和逆矩陣的運算速度，示例代碼：
>>> import numpy as np
>>> from scipy import linalg
>>> m, n = 500, 50
>>> A = np.random.rand(m, m)
>>> B = np.random.rand(m, n)
>>> X1 = linalg.solve(A, B)
>>> X2 = np.dot(linalg.inv(A), B)
>>> print(np.allclose(X1, X2))
>>> %timeit linalg.solve(A, B) 13.3 ms ± 834 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
>>> %timeit np.dot(linalg.inv(A), B) 22.4 ms ± 1.48 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
(3) 特征值和特征向量
n*n的矩陣A可以看作n維空間中的線性變換。若x為n維空間中的一個向量，那么A與x的矩陣乘積就是對x進行線性變換之后的向量。如果x是線性變換的特征向量，那么經過這個線性變換之后，得到的新向量仍然與原來的x保持在同一方向上，但其長度也許會改變。特征向量的長度在該線性變換下縮放的比例稱為特征值。即特征向量x滿足如下等式，λ的值可以是一個任意復數：Ax=λx。
下面以二維平面上的線性變換矩陣為例，演示特征值和特征向量的幾何含義。通過linalg.eig(A)計算矩陣A的兩個特征值evalues和特征向量evectors，在evectors中，每一列是一個特征向量。示例代碼：
下面以二維平面上的線性變換矩陣為例，演示特征值和特征向量的幾何含義。通過linalg.eig(A)計算矩陣A的兩個特征值evalues和特征向量evectors，在evectors中，每一列是一個特征向量。示例代碼：
>>> A = np.array([[1, -0.3], [-0.1, 0.9]])
>>> evalues, evectors = linalg.eig(A)
2.2 擬合與求解optimize模塊
（1）擬合 curve_fit()函數
線性回歸有許多擬合數據的方法，我們將使用curve_fit()函數，它利用的是最小二乘算法。最小二乘算法是一種數學優化技術，在機器學習領域最有名和有效的算法之一。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小。
以下示例中，我們首先從已知函數中生成一些帶有噪聲的數據，然后使用curve_fit()函數擬合這些噪聲數據。示例中的已知函數我們使用一個簡單的線性方程式，即f(x)=ax+b。示例代碼：
以下示例中，我們首先從已知函數中生成一些帶有噪聲的數據，然后使用curve_fit()函數擬合這些噪聲數據。示例中的已知函數我們使用一個簡單的線性方程式，即f(x)=ax+b。示例代碼：
import numpy as np from scipy.optimize
import curve_fit
import matplotlib.pyplot as plt
#創建函數模型用來生成數據
def func(x, a, b): return a*x + b #生成干凈數據
x = np.linspace(0, 10, 100)
y = func(x, 1, 2) #對原始數據添加噪聲
yn = y + 0.9 * np.random.normal(size=len(x))
#使用curve_fit函數擬合噪聲數據
popt, pcov = curve_fit(func, x, yn) #輸出給定函數模型func的最優參數
print(popt)
結果為：
[ 0.99734363 1.96064258]
如果有一個很好的擬合效果，popt返回的是給定模型的最優參數。我們可以使用pcov的值檢測擬合的質量，其對角線元素值代表著每個參數的方差。
>>>print(pcov)
[[ 0.00105056 -0.00525282]
[-0.00525282 0.03519569]]
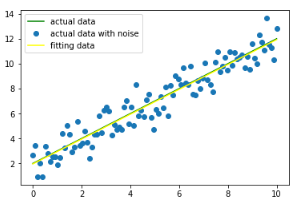
通過以下代碼繪制出了擬合曲線與實際曲線的差異，示例代碼：
yfit = func(x,popt[0],popt[1])
plt.plot(x, y, color="green",label = "actual data")
plt.plot(x, yn, "o", label = "actual data with noise")
plt.plot(x, yfit,color="yellow", label = "fitting data")
plt.legend(loc = "best")
plt.show()
下面做進一步研究，我們可以通過最小二乘擬合高斯分布（Gaussian profile），一種非線性函數：α*exp(-(x-μ)2/2σ2)
在這里，α表示一個標量，μ是期望值，而σ是標準差。示例代碼：
import numpy as np from scipy.optimize
import curve_fit
import matplotlib.pyplot as plt
#創建一個函數模型用來生成數據
def func(x, a, b, c): return (a*np.exp(-(x-b)**2/2*c**2))
#生成原始數據
x = np.linspace(0, 10, 100)
y = func(x, 1, 5, 2)
#對原始數據增加噪聲 yn = y + 0.2*np.random.normal(size=len(x))
#使用curve_fit函數擬合噪聲數據 popt, pcov = curve_fit(func, x, yn)
#popt返回最擬合給定的函數模型func的參數值，如popt[0]=a,popt[1]=b,popt[2]=3
print(popt)
結果為：
[-0.49627942 2.78765808 28.76127826]
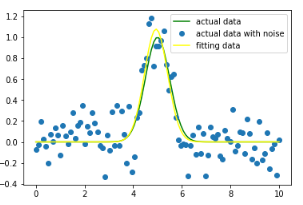
通過以下代碼繪制出了擬合曲線與實際曲線的差異，示例代碼：
p0=[1.2,4,3] #初步猜測參數，如果沒有，默認全為1，即[1,1,1]
popt, pcov = curve_fit(func, x, yn,p0=p0)
#popt返回最擬合給定的函數模型func的參數值，如popt[0]=a,popt[1]=b,popt[2]=3 print(popt)
yfit = func(x,popt[0],popt[1],popt[2])
plt.plot(x, y, color="green",label = "actual data")
plt.plot(x, yn, "o", label = "actual data with noise")
plt.plot(x, yfit, color="yellow", label = "fitting data")
plt.legend(loc = "best")
plt.show()
結果如下圖所示：
通過以上繪圖，我們可以看出對高斯分布函數擬合的效果是可以接受的。
隨著研究的深入，我們可以擬合一個多重高斯分布的一維數據集。現在將這個函數擴展為包含兩個不同輸入值的高斯分布函數。這是一個擬合線性光譜的經典實例，示例代碼如下：
隨著研究的深入，我們可以擬合一個多重高斯分布的一維數據集。現在將這個函數擴展為包含兩個不同輸入值的高斯分布函數。這是一個擬合線性光譜的經典實例，示例代碼如下：
import numpy as np from scipy.optimize
import curve_fit
import matplotlib.pyplot as plt
def func(x, a0, b0, c0, a1, b1, c1):
return a0*np.exp(-(x - b0) ** 2/(2 * c0 ** 2)) + a1 * np.exp(-(x-b1) ** 2/(2 * c1 ** 2))
#生成原始數據
x = np.linspace(0, 20, 200)
y = func(x, 1, 3, 1, -2, 15, 0.5)
#對原始數據增加噪聲
yn = y + 0.9 * np.random.normal(size=len(x))
#如果要擬合一個更加復雜的函數，提供一些估值假設對擬合效果更好
guesses = [1, 3, 1, 1, 15, 1]
#使用curve_fit函數擬合噪聲數據
popt, pcov = curve_fit(func, x, yn, p0=guesses)
#popt返回最擬合給定的函數模型func的參數值，如popt[0]=a,popt[1]=b,popt[2]=3
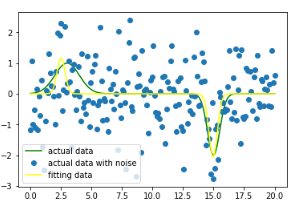
print(popt) yfit = func(x,popt[0],popt[1],popt[2],popt[3],popt[4],popt[5]) plt.plot(x, y, color="green",label = "actual data") plt.plot(x, yn, "o", label = "actual data with noise") plt.plot(x, yfit, color="yellow", label = "fitting data") plt.legend(loc = "best") plt.show()
結果如下圖所示：
（2）最小二乘擬合leastsq()函數
假設有一組實驗數據(x[i], y[i])，我們知道它們之間的函數關系:y = f(x)，通過這些已知信息，需要確定函數中的一些參數項。例如，如果f是一個線型函數f(x) = k*x+b，那么參數k和b就是我們需要確定的值。如果將這些參數用 p 表示的話，那么我們就是要找到一組 p 值使得如下公式中的S函數最小：
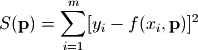這種算法被稱之為最小二乘擬合(Least-square fitting)。optimize模塊提供了實現最小二乘擬合算法的函數leastsq()，leastsq是least square的簡寫，即最小二乘法。下面是用leastsq()對線性函數進行擬合的程序，示例代碼：
import matplotlib.pylab as plt
import numpy as np from scipy
import optimize # 從scipy庫引入optimize模塊 X = np.array([ 8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78 ])
Y = np.array([ 7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05 ])
def residuals(p): #計算以p為參數的直線和原始數據之間的誤差
k, b = p
return Y-(k*X+b)
# leastsq()使得residuals()的輸出數組的平方和最小，參數的初始值為[1, 0]
r = optimize.leastsq(residuals, [1,0])
k, b = r[0] print("k=", k, "b=", b)
結果為：
k = 0.613495349193 b = 1.79409254326
可以通過通過繪圖對比真實數據和擬合數據的誤差，示例代碼；
plt.plot(X, Y, "o", label = "actual data")
plt.plot(X, k*X+b, label = "fitting data")
plt.legend(loc = "best")
plt.show()
結果為：
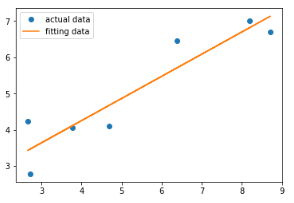
繪圖中的圓點表示真實數據點，實線表示擬合曲線，由此看出擬合參數得到的函數和真實數據大體一致。接下來，用leastsq()對正弦波數據進行擬合，示例代碼：
import numpy as np from scipy.optimize
import leastsq # 從scipy庫的optimize模塊引入leastsq函數
import matplotlib.pyplot as plt # 引入繪圖模塊pylab，并重命名為pl
def func(x, p):
""" 數據擬合所用的函數: A*sin(2*pi*k*x + theta) """
A, k, theta = p
return A*np.sin(2*np.pi*k*x+theta) def residuals(p, y, x):
""" 實驗數據x, y和擬合函數之間的差，p為擬合需要找到的系數 """
return y - func(x, p)
x = np.linspace(0, -2*np.pi, 100)
A, k, theta = 10, 0.34, np.pi/6
# 真實數據的函數參數 y0 = func(x, [A, k, theta])
# 真實數據 y1 = y0 + 2 * np.random.randn(len(x))
# 加入噪聲之后的實驗數據，噪聲是服從標準正態分布的隨機量
p0 = [7, 0.2, 0]
# 第一次猜測的函數擬合參數
# 調用leastsq進行數據擬合
# residuals為計算誤差的函數
# p0為擬合參數的初始值 # args為需要擬合的實驗數據
plsq = leastsq(residuals, p0, args=(y1, x))
print ("actual parameter:", [A, k, theta])
# 真實參數
print ("fitting parameter", plsq[0])
# 實驗數據擬合后的參數
plt.plot(x, y0, label="actual data")
# 繪制真實數據
plt.plot(x, y1, label="experimental data with noise")
# 帶噪聲的實驗數據
plt.plot(x, func(x, plsq[0]), label="fitting data")
# 擬合數據 plt.legend()
plt.show()
這個例子中我們要擬合的函數是一個正弦波函數，它有三個參數 A, k, theta ，分別對應振幅、頻率、相角。假設我們的實驗數據是一組包含噪聲的數據 x, y1，其中y1是在真實數據y0的基礎上加入噪聲的到了。通過leastsq函數對帶噪聲的實驗數據x, y1進行數據擬合，可以找到x和真實數據y0之間的正弦關系的三個參數： A, k, theta。下面是程序的輸出：
>>>actual parameter: [10, 0.34, 0.5235987755982988]
>>>fitting parameter [ 10.12646889 0.33767587 0.48944317]
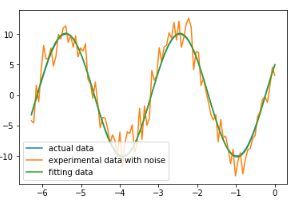
（3）標量函數極值求解fmin()函數
首先定義以下函數，然后繪制它，示例代碼：
import numpy as np from scipy
import optimize import matplotlib.pyplot as plt
def f(x): return x**2 + 10*np.sin(x)
x = np.arange(-10, 10, 0.1)
plt.plot(x, f(x))
plt.show()
結果如下圖所示：
如圖所示，該函數大約在-1.3有個全局最小值，在3.8有個局部最小值。找到這個函數最小值一般而有效的方法是從初始點使用梯度下降法。BFGS算法是做這個的好方法，BFGS算法被認為是數值效果最好的擬牛頓法，是由Broyden，Fletcher，Goldfarb，Shanno四個人分別提出的，故稱為BFGS校正。具體算法思想及解釋請查閱相關資料，這里直接通過optimize.fmin_bfgs()函數求解最小值，示例代碼：
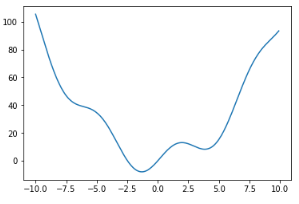
>>> optimize.fmin_bfgs(f, 0)
Optimization terminated successfully. Current function value: -7.945823 Iterations: 5 Function evaluations: 24 Gradient evaluations: 8 array([-1.30644003])
這個方法一個可能的問題在于，如果函數有局部最小值，算法會因初始點不同找到這些局部最小而不是全局最小，示例代碼：
>>> optimize.fmin_bfgs(f, 3, disp=0)#disp是布爾型數據，如果為1，打印收斂消息
array([ 3.83746663])
如果我們不知道全局最小值的鄰近值來選定初始點，我們需要借助于耗費資源些的全局優化。為了找到全局最小點，最簡單的算法是蠻力算法，該算法求出給定格點的每個函數值。示例代碼：
>>>grid = (-10, 10, 0.1)
>>>xmin_global = optimize.brute(f, (grid, ))
>>>xmin_global
array([-1.30641113])
對于大點的格點，scipy.optimize.brute()變得非常慢。scipy.optimize.anneal()提供了使用模擬退火的替代函數。對已知的不同類別全局優化問題存在更有效率的算法，但這已經超出scipy的范圍。為了找到局部最小，我們把變量限制在(0,10)之間，使用scipy.optimize.fminbound()，示例代碼：
>>> xmin_local = optimize.fminbound(f, 0, 10)
>>> xmin_local 3.8374671...
下面的程序通過求解卷積的逆運算演示fmin的功能。對于一個離散線性時不變系統h, 如果輸入是x，那么其輸出y可以用x和h的卷積表示：
現在的問題是如果已知系統的輸入x和輸出y，如何計算系統的傳遞函數h；或者如果已知系統的傳遞函數h和系統的輸出y，如何計算系統的輸入x。這種運算被稱為反卷積運算，是十分困難的，特別是在實際的運用中，測量系統的輸出總是存在誤差的。下面用fmin計算反卷積，這種方法只能用在很小規模的數列之上，因此沒有很大的實用價值，不過用來評價fmin函數的性能還是不錯的。示例代碼：
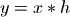
import scipy.optimize as opt
import numpy as np
def test_fmin_convolve(fminfunc, x, h, y, yn, x0): """ x (*) h = y, (*)表示卷積 yn為在y的基礎上添加一些干擾噪聲的結果 x0為求解x的初始值 """ def convolve_func(h): """ 計算 yn - x (*) h 的power fmin將通過計算使得此power最小 """
return np.sum((yn - np.convolve(x, h))**2)
# 調用fmin函數，以x0為初始值
h0 = fminfunc(convolve_func, x0)
print fminfunc.__name__
print "---------------------"
# 輸出 x (*) h0 和 y 之間的相對誤差
print "error of y:", np.sum((np.convolve(x, h0)-y)**2)/np.sum(y**2)
# 輸出 h0 和 h 之間的相對誤差
print "error of h:", np.sum((h0-h)**2)/np.sum(h**2)
print def test_n(m, n, nscale): """ 隨機產生x, h, y, yn, x0等數列，調用各種fmin函數求解b
m為x的長度, n為h的長度, nscale為干擾的強度 """ x = np.random.rand(m) h = np.random.rand(n) y = np.convolve(x, h) yn = y + np.random.rand(len(y)) * nscale x0 = np.random.rand(n) test_fmin_convolve(opt.fmin, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_powell, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_cg, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_bfgs, x, h, y, yn, x0) test_n(200, 20, 0.1)
運行結果為：
import scipy.optimize as opt
import numpy as np
def test_fmin_convolve(fminfunc, x, h, y, yn, x0): """ x (*) h = y, (*)表示卷積 yn為在y的基礎上添加一些干擾噪聲的結果 x0為求解x的初始值 """
def convolve_func(h): """ 計算 yn - x (*) h 的power fmin將通過計算使得此power最小 """
return np.sum((yn - np.convolve(x, h))**2)
# 調用fmin函數，以x0為初始值
h0 = fminfunc(convolve_func, x0)
print fminfunc.__name__
print "---------------------"
# 輸出 x (*) h0 和 y 之間的相對誤差
print "error of y:", np.sum((np.convolve(x, h0)-y)**2)/np.sum(y**2)
# 輸出 h0 和 h 之間的相對誤差
print "error of h:", np.sum((h0-h)**2)/np.sum(h**2)
print def test_n(m, n, nscale): """ 隨機產生x, h, y, yn, x0等數列，調用各種fmin函數求解b m為x的長度, n為h的長度, nscale為干擾的強度 """ x = np.random.rand(m) h = np.random.rand(n) y = np.convolve(x, h) yn = y + np.random.rand(len(y)) * nscale x0 = np.random.rand(n) test_fmin_convolve(opt.fmin, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_powell, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_cg, x, h, y, yn, x0) test_fmin_convolve(opt.fmin_bfgs, x, h, y, yn, x0) test_n(200, 20, 0.1)
（4）函數求解fsolve()
optimize庫中的fsolve函數可以用來對非線性方程組進行求解，其基本調用形式是
fsolve(func, x0)
- func是用于定義需求解的非線性方程組的函數文件名
- x0為未知數矢量的初始值。
首先通過一個簡單的示例，利用fsolve()函數求解當線性函數為0時，x的值，示例代碼：
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
import numpy as np
line = lambda x:x+3 solution = fsolve(line, -2) print(solution)
結果為：
[-3，]
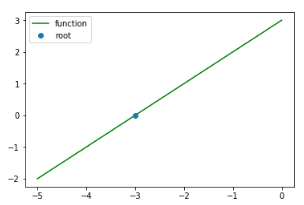
通過以下繪圖函數可以看出當函數等于0時，x軸的坐標值為-3，示例代碼：
x = np.linspace(-5.0, 0, 100)
plt.plot(x,line(x), color="green",label = "function")
plt.plot(solution,line(solution), "o", label = "root")
plt.legend(loc = "best")
plt.show()
結果為：
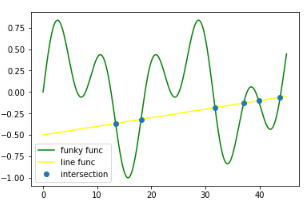
下面我們通過一個簡單的示例介紹一下兩個方程交點的求解方法，示例代碼：
from scipy.optimize
import fsolve
import numpy as np import matplotlib.pyplot as plt
# 定義解函數
def findIntersection(func1, func2, x0):
return fsolve(lambda x: func1(x)-func2(x),x0)
# 定義兩方程 funky = lambda x : np.cos(x / 5) * np.sin(x / 2)
line = lambda x : 0.01 * x - 0.5
# 定義兩方程交點的取值范圍
x = np.linspace(0, 45, 1000)
result = findIntersection(funky, line, [15, 20, 30, 35, 40, 45])
# 輸出結果 print(result, line(result))
plt.plot(x,funky(x), color="green",label = "funky func")
plt.plot(x,line(x), color="yellow",label = "line func")
plt.plot(result,line(result), "o", label = "intersection")
plt.legend(loc = "best")
plt.show()
結果為：
如果要對如下方程組進行求解的話：
- f1(u1,u2,u3) = 0
- f2(u1,u2,u3) = 0
- f3(u1,u2,u3) = 0
def func(x):
u1,u2,u3 = x return [f1(u1,u2,u3), f2(u1,u2,u3), f3(u1,u2,u3)]
下面是一個實際的例子，求解如下方程組的解：
- 5*x1 + 3 = 0
- 4*x0*x0 - 2*sin(x1*x2) = 0
- x1*x2 - 1.5 = 0
from scipy.optimize import fsolve from math import sin,cos def f(x):
x0 = float(x[0])
x1 = float(x[1])
x2 = float(x[2]) return [ 5*x1+3, 4*x0*x0 - 2*sin(x1*x2),
x1*x2 - 1.5 ]
result = fsolve(f, [1,1,1]) print (result)
結果為：
[-0.70622057 -0.6 -2.5 ]
2.3 插值interpolate模塊
插值是離散函數逼近的重要方法，利用它可通過函數在有限個點處的取值狀況，估算出函數在其他點處的近似值。與擬合不同的是，要求曲線通過所有的已知數據。SciPy的interpolate模塊提供了許多對數據進行插值運算的函數，范圍涵蓋簡單的一維插值到復雜多維插值求解。當樣本數據變化歸因于一個獨立的變量時，就使用一維插值；反之樣本數據歸因于多個獨立變量時，使用多維插值。
計算插值有兩種基本的方法，1、對一個完整的數據集去擬合一個函數；2、對數據集的不同部分擬合出不同的函數，而函數之間的曲線平滑對接。第二種方法又叫做仿樣內插法，當數據擬合函數形式非常復雜時，這是一種非常強大的工具。我們首先介紹怎樣對簡單函數進行一維插值運算，然后進一步深入比較復雜的多維插值運算。
（1）一維插值
計算插值有兩種基本的方法，1、對一個完整的數據集去擬合一個函數；2、對數據集的不同部分擬合出不同的函數，而函數之間的曲線平滑對接。第二種方法又叫做仿樣內插法，當數據擬合函數形式非常復雜時，這是一種非常強大的工具。我們首先介紹怎樣對簡單函數進行一維插值運算，然后進一步深入比較復雜的多維插值運算。
interp1d(x, y, kind='linear', ...)
其中，x和y參數是一系列已知的數據點，kind參數是插值類型，可以是字符串或整數，它給出插值的B樣條曲線的階數，候選值及作用下表所示：
| 候選值 | 作用 |
| ‘zero’ 、'nearest' | 階梯插值，相當于0階B樣條曲線 |
| ‘slinear’ 、'linear' | 線性插值，用一條直線連接所有的取樣點，相當于一階B樣條曲線 |
| ‘quadratic’ 、'cubic' | 二階和三階B樣條曲線，更高階的曲線可以直接使用整數值指定 |
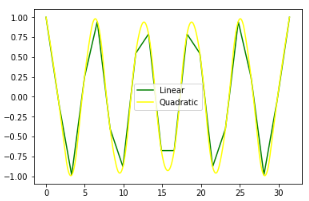
import numpy as np from scipy.interpolate
import interp1d import matplotlib.pyplot as plt
#創建待插值的數據 x = np.linspace(0, 10*np.pi, 20)
y = np.cos(x)
# 分別用linear和quadratic插值
fl = interp1d(x, y, kind='linear')
fq = interp1d(x, y, kind='quadratic')
#設置x的最大值和最小值以防止插值數據越界
xint = np.linspace(x.min(), x.max(), 1000)
yintl = fl(xint)
yintq = fq(xint)
plt.plot(xint,fl(xint), color="green", label = "Linear")
plt.plot(xint,fq(xint), color="yellow", label ="Quadratic")
plt.legend(loc = "best")
plt.show()
結果如下圖所示：
（2）噪聲數據插值
我們可以通過interpolate模塊中UnivariateSpline()函數對含有噪聲的數據進行插值運算，示例代碼：
import numpy as np from scipy.interpolate
import UnivariateSpline import matplotlib.pyplot as plt
# 通過人工方式添加噪聲數據
sample = 30 x = np.linspace(1, 10*np.pi, sample)
y = np.cos(x) + np.log10(x) + np.random.randn(sample)/10
# 插值，參數s為smoothing factor
f = UnivariateSpline(x, y, s=1)
xint = np.linspace(x.min(), x.max(), 1000)
yint = f(xint)
plt.plot(xint,f(xint), color="green", label = "Interpolation")
plt.plot(x, y, color="yellow", label ="Original")
plt.legend(loc = "best")
plt.show()
需要說明的是：在UnivariateSpline()函數中，參數s是平滑向量參數，被用來擬合還有噪聲的數據。如果參數s=0，將忽略噪聲對所有點進行插值運算。結果如下圖所示：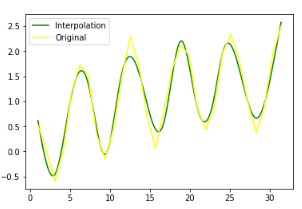
（3）多維插值
多維插值主要用于重構圖片，interpolate模塊中的griddata()函數有很強大的處理多維散列取樣點進行插值運算的能力。其調用形式如下：
griddata(points, values, xi, method='linear', fill_value=nan)
其中points表示K維空間中的坐標，它可以是形狀為(N,k)的數組，也可以是一個有k個數組的序列，N為數據的點數。values是points中每個點對應的值。xi是需要進行插值運算的坐標，其形狀為(M,k)。method參數有三個選項：'nearest'、 ‘linear’、 'cubic'，分別對應0階、1階以及3階插值。以下示例利用1000個隨機散列點對1000x1000像素的圖片進行重構，示例代碼：
import numpy as np from scipy.interpolate
import griddata#定義一個函數
def ripple(x,y):
return np.sqrt(x**2 + y**2) + np.sin(x**2 + y**2)
# 生成grid數據，復數定義了生成grid數據的step，若無該復數則step為5
grid_x, grid_y = np.mgrid[0:5:1000j, 0:5:1000j]
# 生成待插值的樣本數據 points = np.random.rand(1000,2)
value = ripple(points[:,0]*5,points[:,1]*5)
# 用nearest方法插值
grid_z0 = griddata(points*5,value, (grid_x,grid_y),method='nearest')
我們還可以使用interpolate模塊的SmoothBivariateSpline類進行多元仿樣插值運算，對圖片進行重構。示例代碼：
import numpy as np from scipy.interpolate
import SmoothBivariateSpline as SBS #定義一個函數
def ripple(x,y):
return np.sqrt(x**2 + y**2) + np.sin(x**2 + y**2)
# 生成grid數據，復數定義了生成grid數據的step，若無該復數則step為5
grid_x, grid_y = np.mgrid[0:5:1000j, 0:5:1000j]
# 生成待插值的樣本數據 points = np.random.rand(1000,2)
value = ripple(points[:,0]*5,points[:,1]*5)
# 用nearest方法插值
fit = SBS(points[:,0]*5, points[:,1]*5, value, s=0.01, kx=4, ky=4)
interp = fit(np.linspace(0, 5, 1000), np.linspace(0, 5, 1000))
我們得到了一個與上個示例同樣的結果。整體上SmoothBivariateSpline函數的表現略好于griddata函數。
通過反復測試，盡管SmoothBivariateSpline表現略好，但其對給定的樣本數據非常敏感，就可能導致忽略一些顯著特征。而griddata函數有很強的魯棒性，不管給定的數據樣本，能夠合理的進行插值運算。
通過反復測試，盡管SmoothBivariateSpline表現略好，但其對給定的樣本數據非常敏感，就可能導致忽略一些顯著特征。而griddata函數有很強的魯棒性，不管給定的數據樣本，能夠合理的進行插值運算。
NumPy庫已經提供了一些基本的統計函數，如求期望、方差、中位數、最大值和最小值等。示例代碼：
import numpy as np
#構建一個1000個隨機變量的數組
x = np.random.randn(1000)
#對數組元素的值進行統計 mean = x.mean()
std = x.std()
var = x.var() print(mean,std,var)
結果為：
(0.02877273942510088, 0.97623362287515114, 0.95303208643194282)
mean是期望值，std是標準差，var是方差，使用numpy.array對象已有的方法獲得統計指標快速有效，而SciPy庫則提供了更高級的統計工具，它的Stats模塊包含了多種概率分布的隨機變量（隨機變量是指概率論中的概念，不是Python中的變量），其中隨機變量又分為連續和離散兩種。所有的連續隨機變量都是rv_continuous的派生類的對象，而所有的離散隨機變量都是rv_discrete的派生類的對象。
（1）連續概率分布SciPy的stats模塊提供了大約80種連續隨機變量和10多種離散分布變量，這些分布都依賴于numpy.random函數。可以通過如下語句獲得stats模塊中所有的連續隨機變量，示例代碼：
from scipy import stats
[k for k, v in stats.__dict__.items() if isinstance(v, stats.rv_continuous)]
運行結果為：
['ksone', 'kstwobign', 'norm', 'alpha', 'anglit', 'arcsine', 'beta', 'betaprime',
'bradford', 'burr', 'burr12', 'fisk', 'cauchy', 'chi', 'chi2', 'cosine', 'dgamma',
'dweibull', 'expon', 'exponnorm', 'exponweib', 'exponpow', 'fatiguelife', 'foldcauchy',
'f', 'foldnorm', 'frechet_r', 'weibull_min', 'frechet_l', 'weibull_max', 'genlogistic',
'genpareto', 'genexpon', 'genextreme', 'gamma', 'erlang', 'gengamma', 'genhalflogistic',
'gompertz', 'gumbel_r', 'gumbel_l', 'halfcauchy', 'halflogistic', 'halfnorm', 'hypsecant',
'gausshyper', 'invgamma', 'invgauss', 'invweibull', 'johnsonsb', 'johnsonsu', 'laplace',
'levy', 'levy_l', 'levy_stable', 'logistic', 'loggamma', 'loglaplace', 'lognorm', 'gilbrat',
'maxwell', 'mielke', 'kappa4', 'kappa3', 'nakagami', 'ncx2', 'ncf', 't', 'nct', 'pareto', 'lomax',
'pearson3', 'powerlaw', 'powerlognorm', 'powernorm', 'rdist', 'rayleigh', 'reciprocal', 'rice'
, 'recipinvgauss', 'semicircular', 'skewnorm', 'trapz', 'triang', 'truncexpon', 'truncnorm',
'tukeylambda', 'uniform', 'vonmises', 'vonmises_line', 'wald', 'wrapcauchy', 'gennorm', 'halfgennorm']
連續隨機變量對象主要使用如下方法，下表所示：
| 方法名 | 全稱 | 功能 |
| rvs | Random Variates of given type | 對隨機變量進行隨機取值，通過size參數指定輸出數組的大小 |
| Probability Density Function | 隨機變量的概率密度函數 | |
| cdf | Cumulative Distribution Function | 隨機變量的累積分布函數，它是概率密度函數的積分 |
| sf | Survival function | 隨機變量的生存函數，它的值是1-cdf(t) |
| ppf | Percent point function | 累積分布函數的反函數 |
| stats | statistics | 計算隨機變量的期望值和方差 |
| fit | fit | 對一組隨機取樣進行擬合，找出最適合取樣數據的概率密度函數的系數 |
from scipy import stats
# 設置正態分布參數，其中loc是期望值參數，scale是標準差參數
X = stats.norm(loc=1.0, scale=2.0)
# 計算隨機變量的期望值和方差 print(X.stats())
結果為：
(array(1.0), array(4.0))
以上代碼說明，norm可以像函數一樣調用，通過loc和scale參數可以指定隨機變量的偏移和縮放參數。對于正態分布的隨機變量來說，這兩個參數相當于指定其期望值和標準差，標準差是方差的算術平方根。X的stats()方法，可以計算隨機變量X分布的特征值，如期望值和方差。
此外，通過調用隨機變量X的rvs()方法，可以得到包含一萬次隨機取樣值的數組x，然后調用NumPy的mean()和var()計算此數組的均值和方差，其結果符合隨機變量X的特性，示例代碼：
此外，通過調用隨機變量X的rvs()方法，可以得到包含一萬次隨機取樣值的數組x，然后調用NumPy的mean()和var()計算此數組的均值和方差，其結果符合隨機變量X的特性，示例代碼：
#對隨機變量取10000個值
x = X.rvs(size=10000) print(np.mean(x), np.var(x))
結果為：
(1.0287787687588861, 3.9944276709242805)
使用fit()方法對隨機取樣序列x進行擬合，它返回的是與隨機取樣值最吻合的隨機變量參數，示例代碼：
#輸出隨機序列的期望值和標準差
print(stats.norm.fit(x))
結果為：
(1.0287787687588861, 1.998606432223283)
在下面的例子中，計算取樣值x的直方圖統計以及累計分布，并與隨機變量的概率密度函數和累積分布函數進行比較。示例代碼：
pdf, t = np.histogram(x, bins=100, normed=True)
t = (t[:-1]+t[1:])*0.5 cdf = np.cumsum(pdf) * (t[1] - t[0])
p_error = pdf - X.pdf(t)
c_error = cdf - X.cdf(t)
print("max pdf error: {}, max cdf error: {}".format(np.abs(p_error).max(), np.abs(c_error).max()))
運行結果如下所示：
max pdf error: 0.0208405611169, max cdf error: 0.0126874590568
通過繪圖的方式查看概率密度函數求得的理論值（theory value）和直方圖統計值（statistic value），可以看出二者是一致的，示例代碼：
import pylab as pl
pl.plot(t, pdf, color="green", label = "statistic value")
pl.plot(t, X.pdf(t), color="yellow", label ="theory value")
pl.legend(loc = "best")
pl.show()
結果見下圖所示：
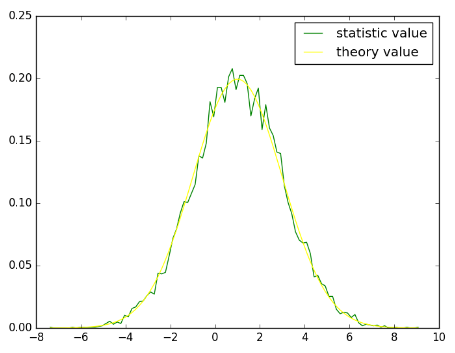
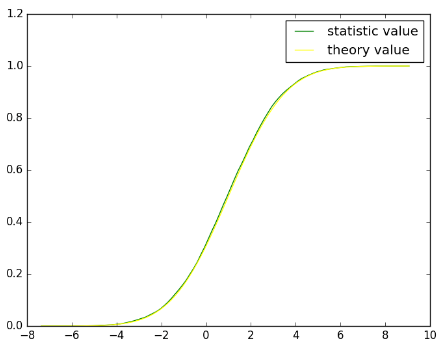
也可以用同樣的方式顯示隨機變量X的累積分布和數組pdf的累加結果，示例代碼：
pl.plot(t, cdf, color="green", label = "statistic value")
pl.plot(t, X.cdf(t), color="yellow", label ="theory value")
pl.legend(loc = "best")
pl.show()
結果為：
p = (0.4, 0.2, 0.1, 0.1, 0.1, 0.1)
# 創建表示這個骰子的隨機變量dice，調用其rvs()方法投擲此骰子20次，獲得符合概率p的隨機數
dice = stats.rv_discrete(values=(x, p))
print(dice.rvs(size=20))
運行結果：
array([3, 6, 4, 5, 5, 2, 1, 3, 3, 1, 1, 3, 1, 5, 1, 3, 4, 1, 2, 2])
除了自定義離散概率分布，我們也可以利用stats模塊里的函數定義各種分布。下面以生成幾何分布為例，其函數是geom()，示例代碼：
import numpy as np from scipy.stats
cdf = dist.cdf(x)
# 生成500個隨機數
sample = dist.rvs(500)
（3）描述與檢驗函數
SciPy中有超過60種統計函數。stats模塊包括了諸如kstest 和normaltest等樣本測試函數，用來檢測樣本是否服從某種分布。在使用這些工具前，要對數據有較好的理解，否則可能會誤讀它們的結果。樣本分布檢驗為例，示例代碼：
import numpy as np from scipy
import stats
# 生成包括100個服從正態分布的隨機數樣本
sample = np.random.randn(100)
# 用normaltest檢驗原假設
out = stats.normaltest(sample)
print('normaltest output')
print('Z-score = ' + str(out[0]))
print('P-value = ' + str(out[1]))
# kstest 是檢驗擬合度的Kolmogorov-Smirnov檢驗，這里針對正態分布進行檢驗 # D是KS統計量的值，越接近0越好
out = stats.kstest(sample, 'norm')
print('\nkstest output for the Normal distribution')
print('D = ' + str(out[0]))
print('P-value = ' + str(out[1]))
# 類似地可以針對其他分布進行檢驗，例如Wald分布
out = stats.kstest(sample, 'wald')
print('\nkstest output for the Wald distribution')
print('D = ' + str(out[0]))
print('P-value = ' + str(out[1]))
SciPy的stats模塊中還提供了一些描述函數，如幾何平均（gmean）、偏度（skew）、樣本頻數（itemfreq）等。
示例代碼
import stats # 生成包括100個服從正態分布的隨機數樣本
out = stats.hmean(sample[sample > 0])
print('Harmonic mean = ' + str(out))
out = stats.tmean(sample, limits=(-1, 1)) print('\nTrimmed mean = ' + str(out))
# 計算樣本偏度 out = stats.skew(sample) print('\nSkewness = ' + str(out))
print('\nSize = ' + str(out[0]))
print('Min = ' + str(out[1][0]))
print('Max = ' + str(out[1][1]))
print('Mean = ' + str(out[2]))
print('Variance = ' + str(out[3]))
print('Skewness = ' + str(out[4]))
print('Kurtosis = ' + str(out[5]))