C#语言应用于银行家舍入法与传统四舍五入法的比较实验
摘要:在現實中的金融場景中,各個數字有小數點是很常見的事。在數據量少的情況下,小數點后兩位怎么取舍問題不大,但如果數據量多的話,取舍的方法不同,數據在匯總時的誤差也會有很大的差別。通過實驗數據分析,得出銀行家舍入法在數據量大的時候,精確度相對來說要比四舍五入法要好的結論。
關鍵字:銀行家舍入;傳統四舍五入;精準計算
C # language is applied to the banker rounding method was compared with the conventional rounding method experiment
WANG Jia-Liang
Abstract: In reality the financial scene, each number has decimal point is a very common thing. In the case of data quantity is little, how two decimal places trade-off problem is nothing, but if the amount of data, choice of methods, data in summary the error also can have very big difference. By analyzing the experimental data, it is concluded that the banker rounding method in a large quantity of data, accuracy than rounding method relatively good conclusion.Key words: bankers rounding; the traditional round; accurate calculation
1.前言
在現實中的金融場景中,各個數字有小數點是很常見的事。不論是體量大的金融公司還是小的金融公司,只要金融有關,它的金融數字小數點后的位數就會少。小數點后的數字位數越多,越精確,也是常理。不過它給用戶展示時,一般只取舍到小數點后兩位。在數據量少的情況下,小數點后兩位以哪種方式取舍,數據匯總誤差不大,但如果數據量多的話,取舍的方法不同,數據在匯總時的誤差也會有很大的差別。
C#語言是微軟開發的一種面向對象的編程語言,它具有語法簡潔、完整的安全性與錯誤處理以及兼容性與靈活性等特點。本文今天就以C#語言來作為編寫實驗數據生成器的基礎語言,批量生成實驗數據,從而通過幾輪不同量級的數據生成實驗,通過對生成數據的匯總與分析,對比實際計算中,銀行家舍入法與傳統的四舍五入法哪一種舍入法的匯總與原始數據比更為精準。雖然歷史上已經有人證明過銀行家舍入法的優越性,不過出于愛好,自己還是打算親自進行實驗驗證。
2.原理介紹
2.1 四舍五入法
四舍五入即我們常識中的四舍五入。大家都比較熟悉。保留位數的后一位,大于等于5,進一,否則舍去。
例如:
(1)1.234,保留小數點后兩位,結果是1.23。
(2)1.235,保留小數點后兩位,結果是1.24。
2.2 銀行家舍入法
銀行家舍入算法:四舍六入五考慮,五后非零就進一,五后為零看奇偶,五前為偶應舍去,五前為奇要進一。
例如:
(1)1.3651,屬于五后非零就進一,保留小數點后兩位,結果是1.37。
(2)1.3650,屬于五后為零看奇偶,五前為偶應舍去,保留小數點后兩位,結果是1.36。
(3)1.3550,屬于五后為零看奇偶,五前為奇要進一,保留小數點后兩位,結果是1.36。
銀行家舍入是IEEE規定的小數舍入標準之一,也是IEEE目前規定中最優秀的舍入方法,因此所有符合 IEEE 標準的語言都應該實現這種算法。
3.實驗比較
3.1 實驗方法
我們使用程序,生成一定批量的帶有小數點后4位的隨機數,然后通過將這些隨機數求和,同時分別對每個隨機數使用傳統四舍五入法保留小數占后兩位,進行求和,以及分別對每個隨機數使用銀行家舍入法保留小數點后兩位,進行求和,最后對比兩種舍入法求和后和隨機數求和后的數據進行對比,比較哪種舍入法同隨機數求和后的結果最接近。初始生成數據量為1000條,之后生成的數據量級以10倍的比例增加。
3.2 C#語言數據生成器編寫
主要使用C#語言編寫基于控制臺的實驗數據生成器。所使用的IDE(Integrated Development Environment)為Microsoft Visual Studio 2013。所編寫的代碼如下:

根據以上代碼運行顯示效果如下圖1所示,只需要輸入需要生成的隨機數的數量,程序就會自行生成指定數量的隨機數,并求和,同時會分為以傳統四舍五入的方法和銀行家舍入的方法,對原始數據取舍后,并求和。

圖1 代碼運行顯示效果
3.3 實驗過程
數據記錄表如下表1數據記錄表所示。表格中數據量欄位,為生成的帶有小數點后4位的隨機數的數量,樣本數據欄位,為以數據量生成隨機數的和,四舍五入欄位為以生成的各樣本數據以四舍五入的方法保留小數點后兩位的數據求和之后的結果,銀行家欄位為以生成的各樣本數據以銀行家舍入法保留小數點后兩位的數據求和之后的結果。勝出者欄位,是以四舍五入保留小數點后兩位的求和結果,以及銀行家舍入法保留小數點后兩位的求和結果分別同原始數據的求和結果作比較,若四舍五入法更接近原始數據結果,則勝出者填寫-1,若銀行家舍入法更接近原始數據結果,則勝出者填寫1。最后將勝出者欄位求和,如果是負數,則四舍五入法勝出,如果是正數則銀行家法勝出。
表1 數據記錄表
|
數據量 |
樣本數據 |
四舍五入(-1) |
銀行家(1) |
勝出者 |
|
1000 |
499.5879 |
499.5 |
499.49 |
-1 |
|
1000 |
492.0308 |
492.12 |
492.1 |
1 |
|
1000 |
507.0111 |
506.93 |
506.9 |
-1 |
|
1000 |
503.1209 |
503.26 |
503.15 |
1 |
|
1000 |
518.0088 |
517.97 |
517.95 |
-1 |
|
10000 |
4984.8203 |
4985.25 |
4984.89 |
1 |
|
10000 |
4957.3182 |
4958.12 |
4957.71 |
1 |
|
10000 |
5015.7731 |
5015.97 |
5015.6 |
1 |
|
10000 |
5007.4791 |
5008.13 |
5007.71 |
1 |
|
10000 |
4986.1471 |
4986.52 |
4986.19 |
1 |
|
100000 |
49929.589 |
49933.81 |
49930.11 |
1 |
|
100000 |
50055.8525 |
50060.86 |
50057.14 |
1 |
|
100000 |
49865.4771 |
49870.7 |
49867.43 |
1 |
|
100000 |
49917.8423 |
49924.37 |
49920.75 |
1 |
|
100000 |
50144.3218 |
50148.03 |
50144.33 |
1 |
|
1000000 |
499983.7733 |
500029.83 |
499993.3 |
1 |
|
1000000 |
499521.6729 |
499576.42 |
499540.46 |
1 |
|
1000000 |
500346.2036 |
500393.05 |
500357.61 |
1 |
|
1000000 |
499554.854 |
499614.1 |
499577.88 |
1 |
|
1000000 |
500191.542 |
500244.8 |
500209.05 |
1 |
|
10000000 |
4998153.809 |
4998648.96 |
4998287.82 |
1 |
|
10000000 |
5000211.921 |
5000715.05 |
5000353.53 |
1 |
|
10000000 |
4998489.693 |
4998977.45 |
4998614.93 |
1 |
|
10000000 |
4999397.266 |
4999885.97 |
4999524.01 |
1 |
|
10000000 |
4999493.114 |
4999992.22 |
4999632.16 |
1 |
|
19 |
3.4 數據分析
為了方便比較,統一將表1數據記錄表中的樣本數據、四舍五入數據、銀行家數據放大至千萬的數量級,然后,分別求四舍五入法與基準值的差值以及銀行家舍入法與基準值的差值,對比兩者的差值,差值越小越接近真實值。生成的數據表如下表2 與樣本數據差值數據所示。
表2 與樣本數據差值數據
|
與樣本數據差值 |
||||
|
樣本數據 |
四舍五入 |
銀行家 |
四舍五入 |
銀行家 |
|
49958790 |
49950000 |
49949000 |
-8790 |
-9790 |
|
49203080 |
49212000 |
49210000 |
8920 |
6920 |
|
50701110 |
50693000 |
50690000 |
-8110 |
-11110 |
|
50312090 |
50326000 |
50315000 |
13910 |
2910 |
|
51800880 |
51797000 |
51795000 |
-3880 |
-5880 |
|
49848203 |
49852500 |
49848900 |
4297 |
697 |
|
49573182 |
49581200 |
49577100 |
8018 |
3918 |
|
50157731 |
50159700 |
50156000 |
1969 |
-1731 |
|
50074791 |
50081300 |
50077100 |
6509 |
2309 |
|
49861471 |
49865200 |
49861900 |
3729 |
429.0000001 |
|
49929589 |
49933810 |
49930110 |
4220.999999 |
520.9999989 |
|
50055852.5 |
50060860 |
50057140 |
5007.499999 |
1287.499999 |
|
49865477.1 |
49870700 |
49867430 |
5222.9 |
1952.9 |
|
49917842.3 |
49924370 |
49920750 |
6527.7 |
2907.7 |
|
50144321.8 |
50148030 |
50144330 |
3708.2 |
8.199999705 |
|
49998377.3 |
50002983 |
49999330 |
4605.670002 |
952.6700012 |
|
49952167.3 |
49957642 |
49954046 |
5474.71 |
1878.71 |
|
50034620.4 |
50039305 |
50035761 |
4684.639998 |
1140.639998 |
|
49955485.4 |
49961410 |
49957788 |
5924.6 |
2302.6 |
|
50019154.2 |
50024480 |
50020905 |
5325.8 |
1750.799999 |
|
49981538.1 |
49986489.6 |
49982878.2 |
4951.509001 |
1340.109001 |
|
50002119.2 |
50007150.5 |
50003535.3 |
5031.294993 |
1416.094993 |
|
49984896.9 |
49989774.5 |
49986149.3 |
4877.569001 |
1252.369 |
|
49993972.7 |
49998859.7 |
49995240.1 |
4887.038002 |
1267.438001 |
|
49994931.1 |
49999922.2 |
49996321.6 |
4991.055014 |
1390.455014 |
根據與樣本數據差值數據生成柱狀圖,如下圖1 四舍五入與銀行家對比圖所示。
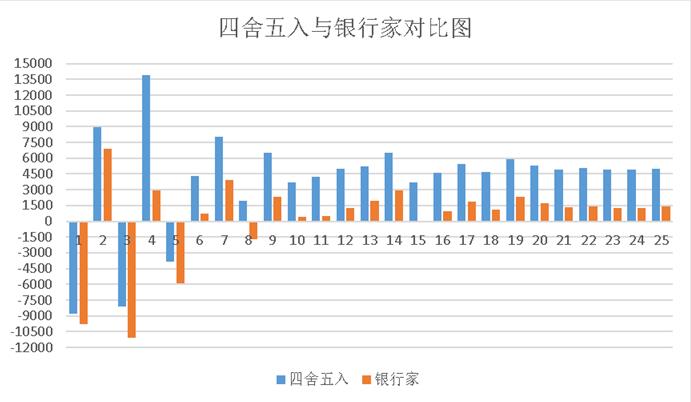
圖2 四舍五入與銀行家對比圖
從圖2四舍五入與銀行家對比圖中,可以明顯看出,在數據量比較少的情況下,四舍五入與銀行家舍入法差別并不是很大,而且在某些時候,甚至比銀行家舍入法更接近樣本數據的真實值。不過,隨著隨機數樣本數量的不斷增加,銀行家舍入法的優勢逐漸體現出來。在實驗進行到第6次的時候,也就是隨機數的樣本數達到10000個的時候,銀行家舍入法就開始呈現更加接近真實樣本數據值的效果。而且之后在第16次的實驗中,也就是數據量達到1百萬時,銀行家舍入法與傳統的四舍五入法相比,與樣本數據真實值的差別顯著縮小。可見,銀行家舍入法,在數據量比較大的時候,效果更為明顯。
4. 結論
4.1 結果分析
從實驗數據上看,銀行家舍入法在數據量大的時候,精確度相對來說要比四舍五入法要好。如果從統計學的角度解釋,那就是“傳統的四舍五入法”使舍入后的結果有的變大,有的變小,而“銀行家舍入法”不像“四舍五入法”那樣逢五就入,使得結果更偏向大數,所以,“銀行家舍入法”則在結果上更平均。如果從概率論的角度來解釋,我們知道,在計算結果中,舍入位數字出現(0-9)的概率可以看作是均等的。那么,四舍五入法,逢五進一的規則,則導致結果中,進的概率,5、6、7、8、9,是0.5,而舍的概率,1、2、3、4,是0.4,可以明顯看出進舍雙方是不均等的。而對于銀行家舍入法,則是更進一步縮小二者之間的概率差距。所以, “銀行家舍入法"比"傳統的四舍五入法"要更為科學,相比四舍五入算法,其優點是:公平性更好。
4.2 不足與完善
實驗本身的不足之處在于樣本數據量仍然不夠多,而且程序設計比較簡單,不夠自動化,程序計算出的結果需要手動錄入Excel中。而且數據樣本數達到1億時,數據竟然超出內存支持的大小。其實實驗方法仍然有很多改進之處,例如換一臺配置更強勁的計算機,同時讓程序將數據自動生成至Excel數據表中,節省了人工錄入的繁瑣。而且實驗次數,不僅僅是現在的25次,可以成倍的增長,以獲取更多的數據,達到更精準的實驗結果。而在現實生活中,例如金融活動中的數據,往往量比較大,結果需要更準確,雖然銀行家舍入法更接近真實值,但在金融的視角,仍然不夠精確。所以,在金融系統的設計中,往往是采用放大和縮小的方法,來獲取更為精準的結果。對于有一些數據,也采用一些簡單的特殊處理。例如:一個用戶借款10000元,三個月,計算每個月還的本金時,結果是3333.33333,但不論你怎么計算,仍然是有誤差的。這個時候,往往采用,前兩期是取平均數,3333.3333,而最后一期則使用 10000-6666.6666= 3333.3334,來消除計算誤差。
其實每一種方法都有每種方法的實際用途,在現實計算中,一定要分析場景,根據具體的場景,來設計有針對性的計算解決方案,這才是最優的解決問題方法。